線形計画から始める数理計画入門

この記事は信州大学のものづくりサークル「kstm」のアドベントカレンダー11日目の投稿です。

普段は組合せ最適化の研究をしている学生です。組合せ最適化って難しそうだよねって思う人もいると思います。僕もそう思います。しかし、世の中にはそんな僕のような人たちを助けてくれるツールがたくさん存在します。その一つに「数理計画ソルバー」が存在します。

そもそも数理計画ってなに？ってなりますよね。ざっくり説明すると数理計画は目的と制約を表す式で記述され、制約の中で目的を最適化(最大化もしくは最小化)します。目的を表す式を目的関数、制約を表す式を制約条件って呼んだりします。

数理計画には様々な分類があります。ここでの分類は、目的関数と制約条件をどのような式で表すかによって分けられています。最も代表的なものは線形計画でしょう。線形計画は、目的関数も制約条件がすべて1次式であるようなものの総称です。線形計画は以下のようなものです。

f:id:wanimaru47:20181210140519p:plain — 式1 : 線形計画問題を一般的に表した式

ベクトルxが線形計画問題の解を表している。もう少し具体的に見てみましょう。

f:id:wanimaru47:20181210222128p:plain — 式2 : 具体的な例

上の例は例1のA, c, b, xの値が次のような場合です。

f:id:wanimaru47:20181210222229p:plain — 式3 : 各変数についての具体値

このような式の作り方(定式化)は解きたい問題によって変わってくるのここでは説明しません。

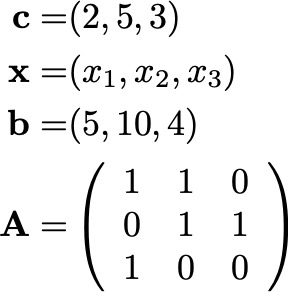
さて、このような問題を線形計画問題へ定式化していかに解くかということが次の問題になります。そこで活躍するのがソルバーです。ソルバーは定式化された問題を広く知られた効率の良いアルゴリズムを用いて解いてくれます。自分でアルゴリズムを設計・実装をしなくていいことが最大の利点でしょう。

ここでは、PuLPと呼ばれるソルバーを用いて実際に問題を解いてみましょう。PuLPはPythonで線形計画などの数理計画の問題を解くことのできるライブラリ(ソルバーのラッパー)です。一番手軽に実行できるので選んでみました。上記の式2をPythonプログラムで書くと以下のようになります。

from pulp import *

prob = LpProblem("Sample", LpMaximize)

# 変数の宣言
x1 = LpVariable("x1", 0, None, LpContinuous)
x2 = LpVariable("x2", 0, None, LpContinuous)
x3 = LpVariable("x3", 0, None, LpContinuous)

c = [2, 5, 3]

A = [[1, 1, 0],[0, 1, 1],[1, 0, 0]]

B = [5, 10, 4]

# はじめに追加した式が「目的関数」
prob += lpDot(c, [x1, x2, x3]) # Maximize : 2 * x_1 + 5 * x_2 + 3 * x_3

# 二つ目以降の式は「制約条件」
for i, b in enumerate(B):
    prob += lpDot(A[i], [x1, x2, x3]) <= B[i]
    
prob.solve()

print(prob)

print("x1 =", x1.value())
print("x2 =", x2.value())
print("x3 =", x3.value())

わざわざ解説することもないぐらいに直感的なライブライになっていると思います。内積はlpDot関数を用いて表すことが出来ます。

これを実際に実行してみると以下のような結果がえられます。x1, x2, x3の値が解になっているわけです。

Sample:
MAXIMIZE
2*x1 + 5*x2 + 3*x3 + 0
SUBJECT TO
_C1: x1 + x2 <= 5

_C2: x2 + x3 <= 10

_C3: x1 <= 4

VARIABLES
x1 Continuous
x2 Continuous
x3 Continuous

x1 = 0.0
x2 = 5.0
x3 = 5.0

変数の宣言は配列ですることも出来ます。配列で宣言する時の例を以下に書いてみました。加えて、lpSum関数(配列に格納されたPuLP変数の総和の式を返す関数)も使っていました。

from pulp import *

prob = LpProblem("Sample", LpMaximize)

# 配列で宣言をした時
X = LpVariable.dicts("x", range(3),  0, None, LpContinuous)

c = [2, 5, 3]

A = [[1, 1, 0],[0, 1, 1],[1, 0, 0]]

B = [5, 10, 4]

# はじめに追加した式が「目的関数」
prob += lpSum([c[i] * X[i] for i in range(3)]) # Maximize : 2 * x_1 + 5 * x_2 + 3 * x_3

# 二つ目以降の式は「制約条件」
for i, b in enumerate(B):
    prob += lpSum([A[i][j] * X[j] for j in range(3)]) <= B[i]
    
prob.solve()

print(prob)

print("x1 =", x1.value())
print("x2 =", x2.value())
print("x3 =", x3.value())